题目

已知:$D$是$BC$的中点,$\angle ADB=60^\circ$,$2\angle ACB=\angle ABC$
求证:$\angle CAB=90^\circ$
知识
- 初中平面几何
P.S.
$\color{red}{\texttt{我的辅助线就不用虚线了}}$
$\color{red}{\texttt{不要小看这道题!!!}}$题解
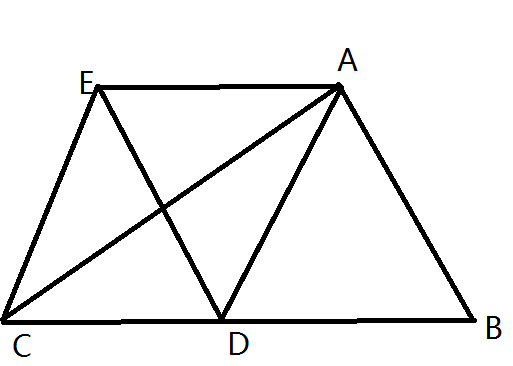
证:
把$\triangle ADB$沿$AD$对折得到$\triangle AED$,连接$EC,ED$
设$\angle ACB=\alpha$,则$\angle ABC=2\alpha$
$\because \angle ADB=90^\circ,\triangle AED \cong \triangle ABD$
$\therefore \angle ADE=\angle ADB=60^\circ$
$\therefore \angle EDC=180^\circ-\angle ADB-\angle ADE=60^\circ$
$\because DE=DB,D$是$BC$的中点
$\therefore ED=DB=DC$
$\therefore \triangle ECD$是正$\triangle$
$\therefore \angle DCE=\angle DEC=60^\circ$
$\therefore \angle ECA=60-\alpha$
$\because \triangle AED \cong \triangle ABD$
$\therefore \angle AED=\angle ABD=2\alpha$
$\therefore \angle EAC=180^\circ-\angle ECA-\angle CED-\angle DEA$
$\qquad\qquad\;=180^\circ-(60^\circ-\alpha)-60^\circ-2\alpha=60^\circ-\alpha$
$\therefore \angle ECA=\angle EAC$
$\therefore EC=EA$
$\therefore AB=EA=EC=CD=DB$
$\therefore \triangle ADB$是正$\triangle$
$\therefore \angle ABD=60^\circ$
$\because \angle ABD=2\alpha$
$\therefore \alpha=30^\circ$
$\therefore \alpha=180^\circ-\angle ACB-\angle ABC$
$\qquad=180^\circ-30^\circ-60^\circ=90^\circ$