题目
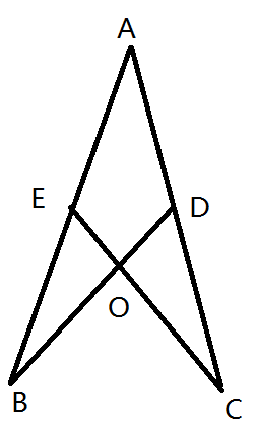
已知:$BD$与$EC$交于$O$,$AE=AD$,$BO=CO$
求证:$AB=AC$
知识
- 初中平面几何
- 三角形内大角对大边
- 正弦函数的单调性
- 正弦定理
P.S.
$\color{red}{\texttt{我的辅助线就不用虚线了}}$
$\color{red}\texttt{不要小看这道题!!!}$题解

证(用反证法):
连接$ED$
假设$\angle OED>\angle ODE$
$\because \angle OED>\angle ODE$
$\therefore OD>OE\Rightarrow -OE>-OD\qquad\qquad(1)$
$\because AE=AD$
$\therefore \angle AED=\angle ADE$
$\therefore \angle BED=\angle CDE$
$\because \angle OED>\angle ODE$
$\therefore \angle C<\angle B$
$\because \angle C,\angle B<90^\circ$ $\therefore \sin c<\sin b$ $\because \frac{ec}{\sin a}="\frac{AE}{\sin" c},\frac{db}{\sin b}$ ad="AE,\sin" a="\sin" a$ ec>AD\qquad\qquad\qquad\qquad\qquad\qquad(2)$
$(2)+(1)\Rightarrow OC>OD$,与题设不符。
$\therefore $原命题成立
证毕